선택 정렬(Selection Sort)이란?

선택 정렬의 원리

정렬되지 않은 원소 중 가장 작은 원소를 찾아 정렬된 요소의 끝에 배치한다. 즉, 배열의 요소 중에서 최소값을 발견한 다음, 이 최소값을 배열의 첫번째 요소와 교환환다. 첫번째 요소를 제외한 나머지 요소들 중에서 가장 작은 값을 선택하고 이를 두번째 요소와 교환한다. 이 과정을 배열이 정렬될 때까지 반복한다. 선택 정렬은 가장 이해하기 쉬운 정렬 방법이고 매번 가장 작은 것을 선택한다는 의미에서 선택 정렬(Selection Sort)이라 한다.

GIF로 보는 선택 정렬

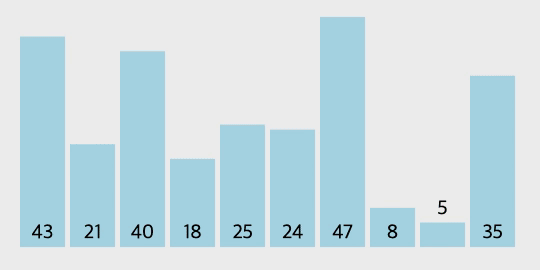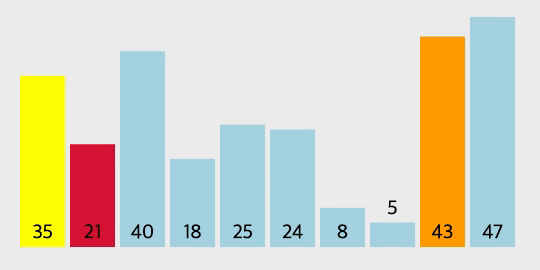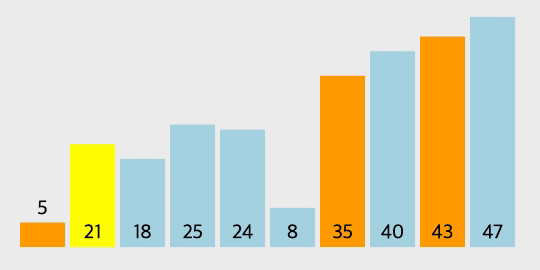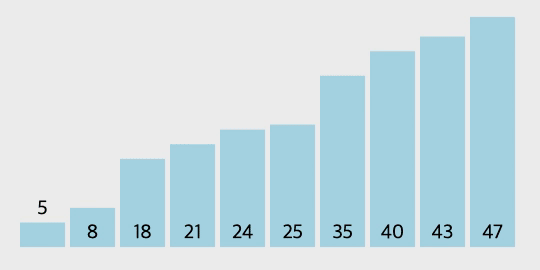
코드 구현

자바스크립트 코드

const selectionSort = dataList => {
  for (let i = 0; i < dataList.length; i++) {
    let minIdx = i;
    for (let j = i + 1; j < dataList.length; j++) {
      if (dataList[minIdx] > dataList[j]) minIdx = j;
    }
    [dataList[minIdx], dataList[i]] = [dataList[i], dataList[minIdx]];
  }
  return dataList;
};

const dataList = [43, 21, 40, 18, 25, 24, 47, 8, 5, 35];
console.log(selectionSort(dataList));
// [5, 8, 18, 21, 24, 25, 35, 40, 43, 47]

파이썬 코드

def selection_sort(data):
    for i in range(len(data)):
        min_idx = i
        for j in range(i + 1, len(data)):
            if data[min_idx] > data[j]:
                min_idx = j
        data[min_idx], data[i] = data[i], data[min_idx]
    return data


data_list = [43, 21, 40, 18, 25, 24, 47, 8, 5, 35]
print(selection_sort(data_list))
# [5, 8, 18, 21, 24, 25, 35, 40, 43, 47]

선택 정렬의 시간 복잡도

선택 정렬은 소스코드 상으로 간단한 형태의 2중 반복문이 사용되었는데 $n-1$번 만큼 가장 작은 값을 찾아서 맨 앞으로 교체해야 한다. 그리고 가장 작은 값을 찾는 과정이 매번 내부 루프안에서 발생한다. 연산 횟수는 $(n - 1) + (n - 2) + ... + 1$로 볼 수 있다. 이는 $n(n - 1) / 2$ 로 표현할 수 있고, 빅오 표기법으로 간단히 $O(n^2)$이라고 표현할 수 있다. 따라서 선택 정렬의 시간 복잡도는 $O(N^2)$ 이다.

선택 정렬의 장단점

장점

• 적은 개수의 원소를 정렬할 때 성능이 좋다.
• in-place 정렬 알고리즘이기 때문에 원소들의 개수보다 무시할만한 저장공간을 더 사용한다(추가적인 메모리 공간 사용이 적다).

단점

• 많은 개수의 데이터를 처리할 때 효율성(efficiency)이 떨어진다.
• 선택 정렬에는 $n$개의 요소를 정렬하기 위한 $n^2$ 단계가 필요하다.

참고

• https://www.fun-coding.org/
• http://dbmspoly.blogspot.com/p/advantage-disadvantages-of-sort.html
• https://visualgo.net/en/sorting
• 이것이 취업을 위한 코딩테스트다
• C언어로 쉽게 풀어쓴 자료구조