BFS에 대해 알아보기 전에 우선 그래프(graph), 큐(queue)에 대한 이해가 필요하다. 그래프에 대한 설명은 [자료구조] 그래프(Graph)란?, 큐에 대한 설명은 [자료구조] JavaScript로 구현하는 큐에 자세히 정리해두었다.

BFS란?

BFS(Breadth First Search)는 너비 우선 탐색이라고 하며 시작 노드로부터 가까운 노드를 먼저 방문하고 멀리 떨어져 있는 노드를 나중에 방문하는 탐색 방법이다. DFS는 최대한 멀리 있는 노드를 우선으로 탐색하는데, BFS는 그 반대다. BFS는 선입선출 방식인 큐 자료구조를 이용하는 것이 일반적이다. 다른 언어의 경우는 보통 내장 라이브러리에 큐를 제공하고 있다. 하지만 자바스크립트는 큐와 관련된 객체가 내장되어 있지 않다. 따라서 큐를 이용하기 위해서는 직접 자료구조를 구현할 필요가 있다.

BFS의 동작 방식

1. 탐색 시작 노드를 큐에 삽입하고 방문 처리한다.
2. 큐에서 노드를 꺼내 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리한다.
3. 2번의 과정을 더 이상 수행할 수 없을 때까지 반복한다.

BFS 구현

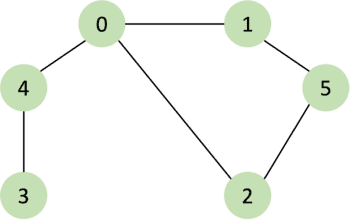
위 그래프를 BFS로 탐색해보자. 인접한 노드가 여러 개 있을 때는 가장 숫자가 작은 노드부터 먼저 큐에 삽입한다고 가정한다.

1. 시작 노드인 0을 큐에 삽입하고 방문 처리를 한다.

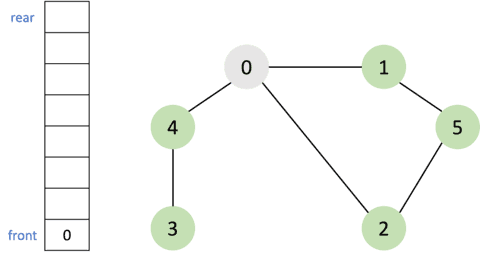
2. 큐에서 0을 꺼내고 방문하지 않은 인접 노드 1,2,4를 큐에 삽입하고 모두 방문 처리를 한다.

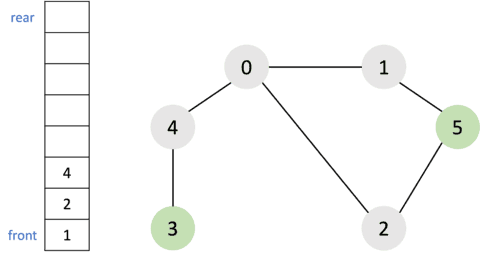
3. 큐에서 1을 꺼내고 방문하지 않은 인접 노드 5를 큐에 삽입하고 방문 처리를 한다.

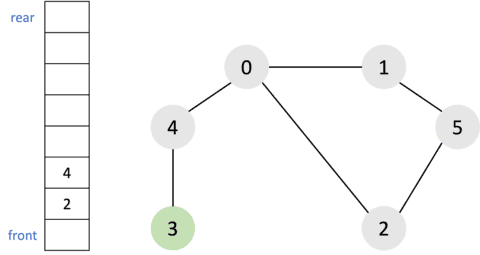
4. 큐에서 2를 꺼내고 방문하지 않은 인접 노드가 없으므로 무시한다.

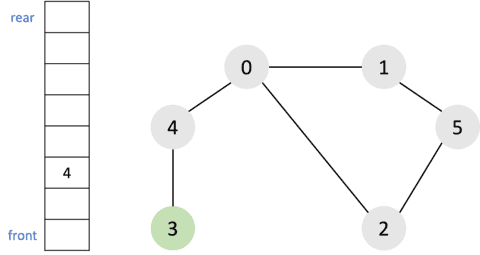
5. 큐에서 4를 꺼내고 방문하지 않은 인접 노드 3을 큐에 삽입하고 방문 처리를 한다.

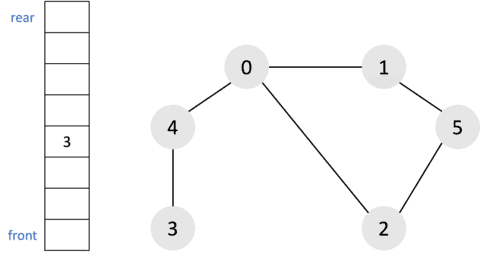
6. 남아 있는 노드에 방문하지 않은 인접 노드가 없다. 따라서 모든 노드를 큐에서 차례대로 꺼낸다.

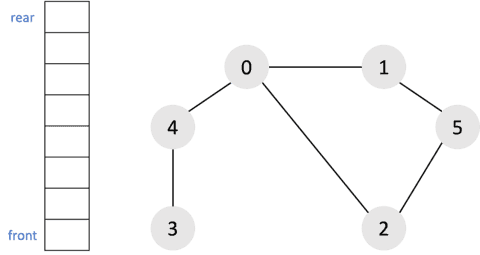
결과적으로 그래프의 탐색 순서는 다음과 같다.
0 → 1 → 2 → 4 → 5 → 3

BFS 구현 코드

function BFS(graph, start, visited) {
  const queue = new Queue();
  queue.push(start);
  visited[start] = true;

  while (queue.size()) {
    const v = queue.popleft();
    console.log(v);

    for (const node of graph[v]) {
      if (!visited[node]) {
        queue.push(node);
        visited[node] = true;
      }
    }
  }
}

const graph = [[1, 2, 4], [0, 5], [0, 5], [4], [0, 3], [1, 2]];
const visited = Array(6).fill(false);
BFS(graph, 0, visited);
// 0 1 2 4 5 3

큐(Queue) 구현 코드

class Queue {
  constructor() {
    this.store = {};
    this.front = 0;
    this.rear = 0;
  }

  size() {
    if (this.store[this.rear] === undefined) {
      return 0;
    } else {
      return this.rear - this.front + 1;
    }
  }

  push(value) {
    if (this.size() === 0) {
      this.store['0'] = value;
    } else {
      this.rear += 1;
      this.store[this.rear] = value;
    }
  }

  popleft() {
    let temp;
    if (this.front === this.rear) {
      temp = this.store[this.front];
      delete this.store[this.front];
      this.front = 0;
      this.rear = 0;
      return temp;
    } else {
      temp = this.store[this.front];
      delete this.store[this.front];
      this.front += 1;
      return temp;
    }
  }
}

BFS의 시간 복잡도

BFS는 그래프가 인접 리스트로 표현되어 있으면 전체 수행시간이 $O(n+e)$이며, 인접 행렬로 표현된 경우는 $O(n^2)$ 시간이 걸린다. BFS도 DFS와 같이 희소 그래프를 사용할 때 인접 리스트를 사용하는 것이 효율적이다.

참고

• 이것이 취업을 위한 코딩테스트다
• C언어로 쉽게 풀어쓴 자료구조